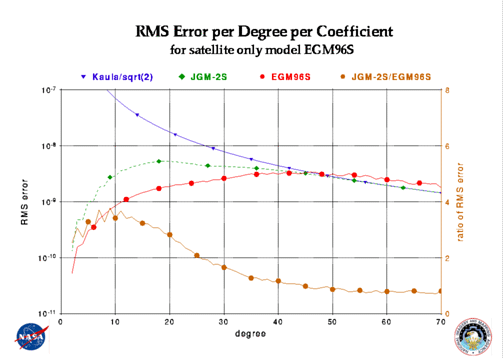
We compare the projected error from the two satellite only solutions, JGM-2S, and the new satellite only solution, EGM96S (the foundation of EGM96). Note, that the error at the higher degrees is higher in EGM96S, since we are using a different a priori constraint than in JGM-2S. All satellite only solutions must be conditioned by the application of a power law constraint, to prevent the high degree terms from developing excessive power (see the discussions of previous satellite only solutions for details; cf. Nerem et al., [1994], and Marsh et al., [1990]). In JGM-2S, the power law constraint that was applied was Kaula's power law, divided by the square root of two. However, this power law underestimates the power in the Earth gravity field, as determined from surface gravity observations. Therefore, we use a a power law constraint derived from the signal of the surface gravity data to spectrally constrain the coefficients of EGM96S. As illustrated in the figure below, the addition of the new tracking data results in a factor of two to four improvement in the formal errors, as measured by the ratio of the coefficient sigmas at the lower degrees. Since the satellite only solution is the foundation of the high degree quadrature solution, it is important that the spectrum of the errors in the satellite only model be consistent with the signal observed by the surface gravity data.
back to table of contents.
back to egm96 home page